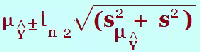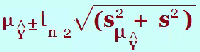|
|||||||
|
Coming to Statistica Phone/iPad apps Group Classes Interactive Webinars Blog Guestbook |
|||||||
|
Please contact Statistica |
|||||||
|
E-mail anne@statistica.com.au Phone (08) 9457 2994Place Willetton, Western AustraliaTwitter @Anne_statistica |
|||||||
 |
||||||||||||||||||||
Mathematics & Statistic Tutor Perth - SPSS Help |
||||||||||||||||||||
|
|
|
|
|
|
|
|
|||||||||||||
|
Chi-Square Test of Independence (a) Write down the linear regression equation. (b) What is the value of the standard error of the estimate? (c) How many degrees of freedom are associated with the t-value for the line of regression? (d) What is the value of the correlation coefficient? (e) Confidence and Prediction Interval (f) What is the 95% confidence interval for the mean value of Ŷ when x = ? (g) What is the 95% prediction interval for Ŷ when x = ? What I have tried to do here is put as simply as possible how to answer a variety of questions using SPSS output. The following tables are an example of the output and then I have shown where the information is to answer certain questions.
Coefficients
Model Summary
ANOVA
(a) Write down the linear regression equation.
Ŷ = b0 + b1x = 2.129 + .338x (b) What is the value of the standard error of the estimate? This has another name the standard deviation of y about the regression line. It tells us how much the observed values differ from the values on the regression line. It gives us an idea of the scatter of the points around the line of regression.
In the formulae for the prediction interval concerning regression, this value is represented by the letter, s (c) How many degrees of freedom are associated with the t-value for the line of regression? This is (n - 2) degrees of freedom and is given in the analysis of variance.
So even without knowing the sample size, you can find the degrees of freedom by looking on the Residual line in the ANOVA. You can, also, state the size of the sample which in this case is 8 (d) What is the value of the correlation coefficient?
The correlation coefficient is given by R and is a measure of the linear association between the variables.
The coefficient of determination, R Square, gives an indication of how good a choice the x-value (independent variable) is in predicting the y-value (dependent variable). It describes the amount of variation in y-values explained by the regression line. The larger the value the better the regression line describes the data.
You would have to look ‘sign of b1’, to check to see if it was positive or negative correlation.
You do not have to worry too much about the adjusted value of R Square as it just takes into account the actual sample size.
Durbin-Watson should be between 1.5 and 2.5 indicating the values are independent.
So the value of the correlation coefficient is 0.941. So the value of the coefficient of determination is 0.886 So the value of the Durbin - Watson is 2.321 (e) Confidence and Prediction Intervals We now have to realise that the predicted value can be viewed in two ways: The mean response of all y values for a particular value of x. 2. The predicted value of y for an individual at a particular value of x. This is written as Ŷ It is still the same number just different symbols!! This information is given in the data window and not the output window.
(f) What is the 95% confidence interval for the mean value of Ŷ when x = ? The confidence interval for the population mean of all y values associated with the value of x chosen. It is similar to all other confidence intervals in its interpretation and it involves a t-value and standard error (sample standard error of predicted value).
This confidence interval is found under the headings “lmci_1” and “umci_1” in the data window. This would give the upper and lower limits of the confidence interval so in an examination, it will probably be a different level of confidence i.e. 90% rather than the output’s 95%. This means that you will look up the 90% t-value in tables. All the other values remain the same so can be found in the output. This value, The value, The “_1” is just in case you have more than one confidence or prediction interval so they can be distinguished from each other. You may be given the value of
(g) What is the 95% prediction interval for Ŷ when x = ? The prediction interval is an interval of a prediction for an individual for a certain value of x. This is more variable than the confidence interval as we are dealing with individuals rather than averages. Here is the formula and you can see the extra term ‘s2’ where The “ This prediction interval is found under the headings “lici_1” and “uici_1” in the data window. This would give the upper and lower limits of the prediction interval so in an examination, it will probably be a different level of prediction i.e. 90% rather than the default output 95%. Once again look up the 90% t-value and substitute in with all the other values from the output. In the output, the symbol “i” is used to denote individual. The value, The value, Ŷ is found in the output under the heading ”pre_1” The value, s, is found in the table below:
Once again you will just have to substitute the values into the equation
The values of Ŷ and I hope you followed this quick explanation of the SPSS output for regression.
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| [Home] |



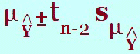
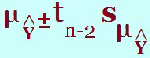 along with the t-value.
along with the t-value.