|
Chi-Square Test of Independence c2
SPSS output for Regression Normal distribution
Summary Notes for Tests of Significance (Critical and P Value)
SPSS Instructions
Hypothesis Testing (Tests of Significance)
In basic statistics units, the examinations will have quite a few questions involving Tests of Significance of one sort or another. So we should try to find a little pattern that we can follow and adapt where necessary.
First of all, recognising the question is a Test of Significance and then spotting which test it is, requires looking at a lot of questions. Use the worked examples in any statistics book to learn how to spot the clues and hints.
Here are some very general points but do read the rest of the question to double check.
The words “ level of significance” or a = 0.05 or 0.01 (these are the usual numbers).
You will be given data and then asked in a variety of different ways whether this data is consistent with a statement concerning the population.
There is a set procedure that you will always have to take when doing these questions. I have a list of steps that I follow each time. The ones in Red are very important, the others are my way of doing things:
Assumptions and Definitions
Hypotheses
Test Data
Test statistic
P-value
Decision
Conclusion
Now these are all grand titles for what we have seen before so do not let them put you off the question.
It is much easier to see all this in action if we have an example:
Can the environment of the examination room have an effect on ability of the student to perform? This was the question posed by the Psychology Department of the University. There are many factors involved here but one lecturer had an interest in scents and put forward the theory that a pleasant floral scent in the room would improve the score on a standardised test.
An experiment was conducted on 25 First Year Students to test this theory. After the test was conducted, the sample mean was found to be 66 with a standard deviation of 2.65. Normally the average score has been 64. Does the floral scent improve the score on the standardised test? Test at the 5% significance level.
Not the question to give any hay fever or allergy sufferers but just keep sniffing and sneezing and we will pull through this together.
First, underline the parts you feel are important then check and see if it matches the words in red.
Can the environment of the examination room have an effect on the student’s ability to perform in a test? This was the question posed by the Psychology Department of the University. There are many factors involved here but one lecturer had an interest in scents and put forward the theory that a pleasant floral scent in the room would improve the score on a standardised test.
An experiment was conducted on 25 First Year Students to test this theory. After the test was conducted, the sample mean was found to be 66 with a standard deviation of 2.65. Normally the average score on this test has been 64. Does the floral scent improve the score on the standardised test? Test at the 5% significance level.
The question being posed is asking us to show that something has changed whether that the situation has improved, worsened or just changed.
For this example, would the test score improve with the floral scent? We are going to use the scores from a sample of 25 students, these have been given as a sample mean and a sample standard deviation so we do not have to do any more calculations.
These scores are going to give us evidence that the floral scent works and improved the test score or evidence that it really did not make any difference to the score whatsoever.
So what is the usual score or the score that has been happening in the past. This is the number that is usually found by itself or the number in the question that is not the sample size, sample mean or sample deviation.
Now the question is asked again, “ Does the floral scent improve the score on the standardised test?”, so we are hoping that the scores are going to get bigger.
The words “ Significance Level” indicate that it is a Test of Significance and here we are using
a = 0.05.
We only have one sample so do not go inventing any more samples.
Let us get started on the steps:
Assumptions and Definitions
Please define the variable that you are going to test so that there is no confusion. This is quite simple and is just achieved in a sentence. For this question, we could say something along the lines:
The variable of interest is the score obtained on the standardised test taken in the room with floral scent.
In the examination, it is not always stated directly but there are certain different assumptions made for each type of test. These assumptions are important especially if you do research later.
We are going to use the normal distribution or t-distribution later for the test statistic so we really need the data to be normally distributed.
This can happen in two ways:
- The population is normally distributed.
- The sample size is large enough for the Central Limit Theorem to help us assume approximate normality.
Without too much detail, we will be using the normal distribution to work out the probability of finding the sample mean in the population stated in the Null Hypothesis.
Just quickly, here is the definition for the Central Limit Theorem (CLT), it states that as the sample size increases the sampling distribution of the sample mean can be approximated by the Normal Distribution. This is regardless of the distribution of the Parent population. The sample size should be at least 25.
We would use a histogram, P - P or Q - Q plot to show that the data is approximately normally distributed, this would only give us an indication that the population is normally distributed. Statistically better though is a Test of Normality such as Kolmogorov -Smirnov or Shapiro-Wilk. I try to say Kolmogorov-Smirnov at least once a week during semester!
Now we will have to assume that the sample is random and not biased in any way as part of the experimental design. We cannot test for this in examinations but we have control of this in real life situations.
So the assumptions for this particular question would be the sample must be random, unbiased and approximately normally distributed.
Hypotheses
Now we are interested in saying something about the population and not the sample, so we will be using population parameters. The hypotheses can either be written in words or symbols.
The number in the hypothesis is the leftover number in the question i.e. it is not the sample size, sample standard deviation or sample mean or the number that states this is what usually happens.
The Null Hypothesis is always written as if nothing has changed and so is always written as “equal to”
So for this question, the Null Hypothesis could be written as follows:
Null Hypothesis: m = 64
Note this value of 64 is the score usually obtained before the test
The Alternative Hypothesis is written as if things are changing in the manner as you think.
We need to look at the words in the question that give us an indication on how we think or propose the variable is changing. The phrases that help us in the question are “... and put forward the theory that a pleasant floral scent in the room would improve the score on a standardised test” or “ Does the floral scent improve the score on the standardised test?”. The word “ improve” implies that the score gets bigger, so we would expect the Alternative Hypothesis to be “ greater than”
So for this question, the Alternative Hypothesis could be written as follows
Alternative Hypothesis m > 64
We could write the hypotheses out in words instead of symbols and it could be as follows:
Testing the Null Hypothesis that the true population score on the standardised test is 64 against the Alternative Hypothesis that the population score on the standardised test is now greater than 64.
Test Data
This part I feel is important as it does let the marker know that you have taken the correct values from the question. It may help you gain extra marks as it looks like you know what you are doing.
`x = 66 Sample Mean
s = 2.65 Sample Standard Deviation
m = 64 Population Mean
a = 0.05 Significance Level
n = 25 Sample Size
Test Statistic
This is just a fancy title for the z-value or t-value. We use t-value when we have the sample standard deviation not the population standard deviation AND the sample size is less than 30. More often than not it is a t-value.
For this example, the test statistic is:
Check to see if you really understand why it is a t-value and not a z-value.
Now substitute the given values and get a value for t
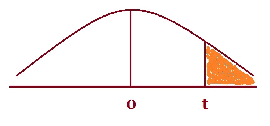
P-value
OK, putting it as simply as possible, the p-value may be written as a ‘ greater than’ probability.
If the t-value or z-value is negative, all you do is ignore the sign and write it as ‘ greater than’ probability in order to calculate the probability.
For our question
We need the degrees of freedom which in this case is n - 1 = 24
You can use your calculator or look the value in the t-tables and this procedure is described below.
Now we look the value in tables (‘ greater than’ probability values)
Down the side are the degrees of freedom.
Across the top is the range of probabilities decreasing as you move to the right.
In the middle are the t values increasing as you move to the right.
Probabilities 0.25 0.20 0.025 etc.. 0.001 0.0005
df
1
2 0.816 1.061 22.33 31.60
etc
24 0.685 0.857 2.064 3.467 3.745
So back to our example: To look for the probability, go down the side until you get to 24 degrees of freedom and then look across the line until you find the numbers nearest the test statistic value.
Now we cannot give an exact value from the tables but we can see that the probability must be smaller than 0.0005. The values of the probability are getting smaller as we go to the right so the next column would be smaller than 0.0005.
So the p-value is smaller than 0.0005, in symbols p-value < 0.0005
Just be careful when you have a “ not equal to” alternative hypothesis you have to multiply by two as you have only found half of the p-value.
Decision
Well, we have to decide whether to Do not reject or Reject the Null Hypothesis.
If the p-value bigger than 0.05 then Do not reject the Null Hypothesis
If the p-value smaller than 0.05 then Reject the Null Hypothesis
Please get this bit correct as you can lose most of your marks here as this is the first part where you have to interpret your result.
So looking at our example we can see that the p-value is much less than 0.05 so we will reject the Null Hypothesis.
Conclusion
This is the second part where you have to interpret your result but this is slightly harder as you have to relate it to the question.
Now I tend to be a bit lazy here and I learn a few sentences and then fit the answer to the question.
Here is the one for this particular example:
The ‘ Rejecting ’ conclusion sentence
The results are statistically significant indicating that there is enough evidence to suggest that floral scent improves the mean score on the standard test at the 5% significance level.
The brown part is my standard sentence.
The purple part, I usually take from the part of the question that tells you the Alternative Hypothesis.
i.e. Does the floral scent improve the mean score on the standard test at the 5% significance level.
The ‘ Do not Rejecting ’ conclusion sentence
The results are not statistically significant indicating that there is not enough evidence to suggest that floral scent improves the mean score on the standard test at the 5% significance level.
The brown part is my standard sentence.
The purple part, I usually take from the part of the question that tells you the Alternative Hypothesis.
i.e. Does floral scent improve the mean score on the standard test at the 5% significance level.
Summary Notes Tests of Significance (Critical and P Value)
|