The farmer has 4,000  m³ of storage space.

Each acre yields an average of 110 m³ of Barley and 30 m³ Wheat. 

The farmer has  available capital of $15 000.

If the net profit per m³ of Barley is $1.30 and for Wheat is $2.00, this is after all expenses  have been subtracted. How should the farmer plant the 100 acres to maximise the  profits?

The first step is to write what the letters are standing for and to do this look at the  question. 
The last sentence helps us  “ How should the farmer plant the 100 acres to maximise the profits?” 
so we need to know how many acres of each crop to plant.
Let x be the  number of acres of Barley planted.
Let y be the  number of acres of Wheat planted.

Sometimes what  the letters are standing for may be given to you.

The second step  look  at the question, we are given some information about how many acres, how much  money and how much storage the farmer has.
In the questions, look for what you are told about the situation
Another hint is put all of  the quantities with the same units together
i.e.  m³, acres  and $.

 “ The farmer has 4 000 m³ of storage space” so how much space does Barley and Wheat need? The question tells us “ Each acre yields an average of 110 m³ of Barley and 30 m³ Wheat”.
Writing this mathematically,

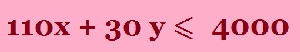“ The farmer has available capital of $15 000.” so his expenses cannot be more than this value ( he has no more money to pay over $1500). 
So we must work out what the expense is for growing each of the crops, look in the table to see the total cost for growing Barley and Wheat.

If x is the number of acres of Barley grown then the cost of growing Barley is  $120 x.
If y is the number of acres of Wheat grown then the cost of growing Wheat is  $210 y.
Combining these bits of information, the farmer cannot spend more than $15 000 and his cost for the crops is (120 x plus 210 y).  
In mathematical terms,

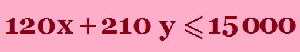“ A farmer has 100 acres on which he can  plant two crops...”
so he can not plant more than 100 acres but sometimes it could be profitable for  him to plant less than 100 acres.
Now we have to write that as a mathematical  statement:

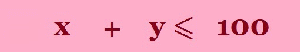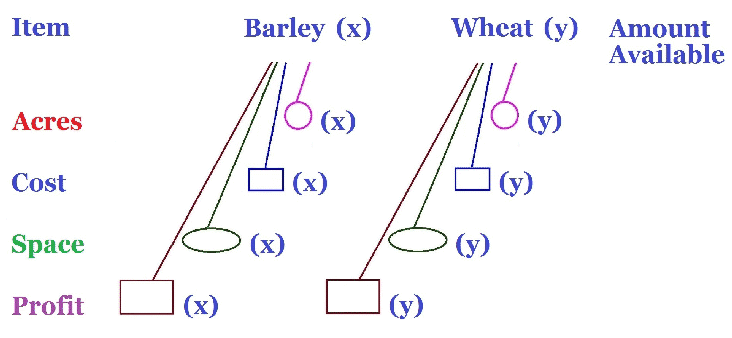
The question asks for the maximum profit the farmer could obtain.
Now some thinking, how do we find the profit for each crop. In the question,

the profit per  m³
“ profit per m³ of Barley is $1.30 and for Wheat is $2.00”

the  average yield for each crop
“ Each acre yields an average of 110 m³ of Barley and  30 m³ of Wheat”

We will multiple these two quantities together for each crop and then  adding the two will give the overall profit for both crops.

So writing this  mathematically,
Profit = (1.30) (110) x + (2.00) (30 ) y

                                     Profit = 143 x +  60 y

Collect all the inequalities together

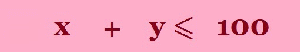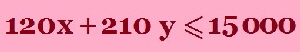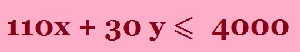Profit = 143 x + 60 y, this is the expression we want to maximise

Here is another way of producing the same inequalities by using the following diagram and filling in the spaces

“ A farmer has 100 acres on which he can  plant two crops...”
so he can not plant more than 100 acres but sometimes it could be profitable for  him to plant less than 100 acres.
We fill the pink circles with how many acres of Barley and Wheat ( x and y respectively) and put the total amount of acres available at the end.

“ The farmer has available capital of $15 000.” so his expenses cannot be more than this value ( he has no more money to pay over $1500). 
So we must work out what the expense is for growing each of the crops, look in the table to see the total cost for growing Barley and Wheat.

The cost of growing Barley is  $120 x.
The cost of growing Wheat is  $210 y.
We fill the blue rectangles with how much it costs to grow Barley and Wheat and that is $120 per acre for Barley and $210 per acre for Wheat and put the money available $ 15 000 at the end.

 “ The farmer has 4 000 m³ of storage space” so how much space does Barley and Wheat need? The question tells us “ Each acre yields an average of 110 m³ of Barley and 30 m³ Wheat”.
We fill the green ovals with how much storage Barley and Wheat take and that is 110m³ and 30m³ respectively and put the available storage, 4 000 at the end.

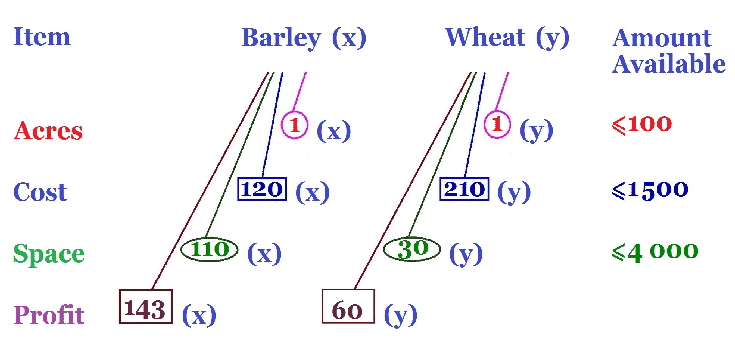
The question asks for the maximum profit the farmer could obtain.
Now some thinking, how do we find the profit for each crop. In the question,

the profit per  m³
“ profit per m³ of Barley is $1.30 and for Wheat is $2.00”

the  average yield for each crop
“ Each acre yields an average of 110 m³ of Barley and  30 m³ of Wheat”

We will multiple these two quantities together for each crop and then  adding the two will give the overall profit for both crops.

We fill the brown rectangles with how much profit from Barley and Wheat, $143 and $60 respectively. There is no number at the end as this is the amount we want to maximise

Collect all the inequalities together

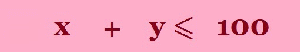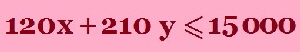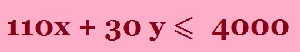Profit = 143 x + 60 y, this is the expression we want to maximise. We have the same inequalities as before just a more picturesque way of finding them.

Now this is where we will get serious and have to graph all these lines on a diagram at one time. Now this is where my diagrams may not look so good due to my lack of artistic computing skills but please try to follow it.

How do we draw the inequalities as lines, we will think of the equations as equal to rather than less than or greater than,
then we will put x = 0 and find out the y-value and then put y = 0 and find out the x-value. These are the y and x intercepts on the graph.

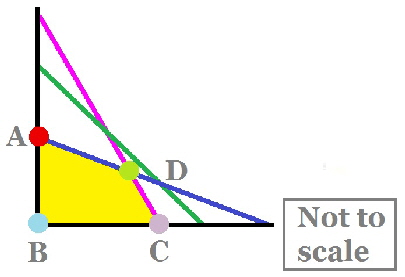
Here is one way to draw the line 110 x + 30 y = 4 000

Let x = 0             so 30 y = 4 000     y = 400 /3   = 133.3

Let y = 0             so 110 x = 4 000   x = 400 /11  =   36.4

Now choose a point to test whether it satisfies the inequality (often I choose (0,0)), if it does then make sure that it is included in the shaded side.

The pink line is    110 x +  30 y    =   4 000

The green line is          x +   y        =   100

The blue line is    120 x + 210 y  =   15 000

The area required is shaded in yellow

The multicoloured dots A, B, C and D are the points of interest as these are the extremes of the shaded area.

We will have to find the co-ordinates of these points, some are easy and others are slightly more difficult!

Point A  x = 0, 

120 x + 210 y  = 15 000,    210 y = 15 000           y = 500 /7 = 71.43

Point B  x = 0   y = 0

Point C  y = 0,      

110 x + 30 y = 4 000,                 110 x = 4 000       x = 400 /11 = 36.36

Point D needs a bit of work as the point is not on any axis.

We will have to solve either on a graphics calculator or simultaneous equations to find the intersection point.

110 x + 30 y    = 4 000                     1   multiply each term by 7

120 x + 210 y = 15 000                    2

770 x + 210 y = 28 000                   3

Equation 3 minus Equation 2

770 x + 210 y   =  28 000             3       

120 x + 210 y   =  15 000              2

650 x = 13 000     so x = 13 000 /650 = 20

Substituting the value of x into equation 1  (any equation would do)

110 (20)       + 30 y   = 4 000

2200            + 30 y   = 4 000

30 y = 1 800     so y = 1 800 /30 = 60.

So the co-ordinates of point D are x = 20 and y = 60.

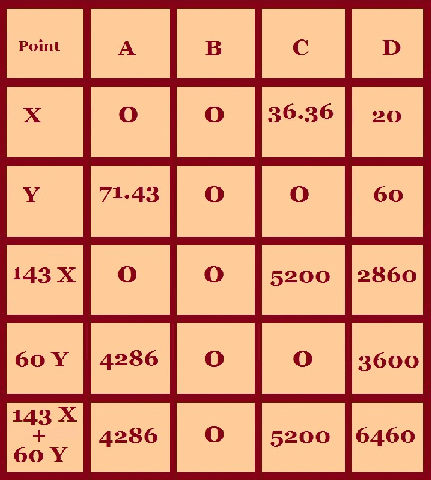
We create the following table by writing in the co-ordinates and then the formula which we want to maximise or minimise. 

If we want to maximise then we choose the largest value and the opposite if we want to minimise i.e. the smallest.

So we can see that the formula, Profit = 143 x + 60 y is a maximum at point D, where x = 20 and y = 60

So the Farmer should plant 20 acres of Barley and 60 acres of Wheat in order to gain a maximum profit of $6460