|
||||
|
Coming to Statistica Phone/iPad apps Group Classes Interactive Webinars Blog Guestbook |
||||
|
Please contact Statistica |
||||
|
E-mail anne@statistica.com.au Phone (08) 9457 2994Place Willetton, Western AustraliaTwitter @Anne_statistica |
||||
 |
|||||||||||||||||||
Mathematics & Statistic Tutor Perth - SPSS Help |
|||||||||||||||||||
|
|
|
|
|
|
|
|
||||||||||||
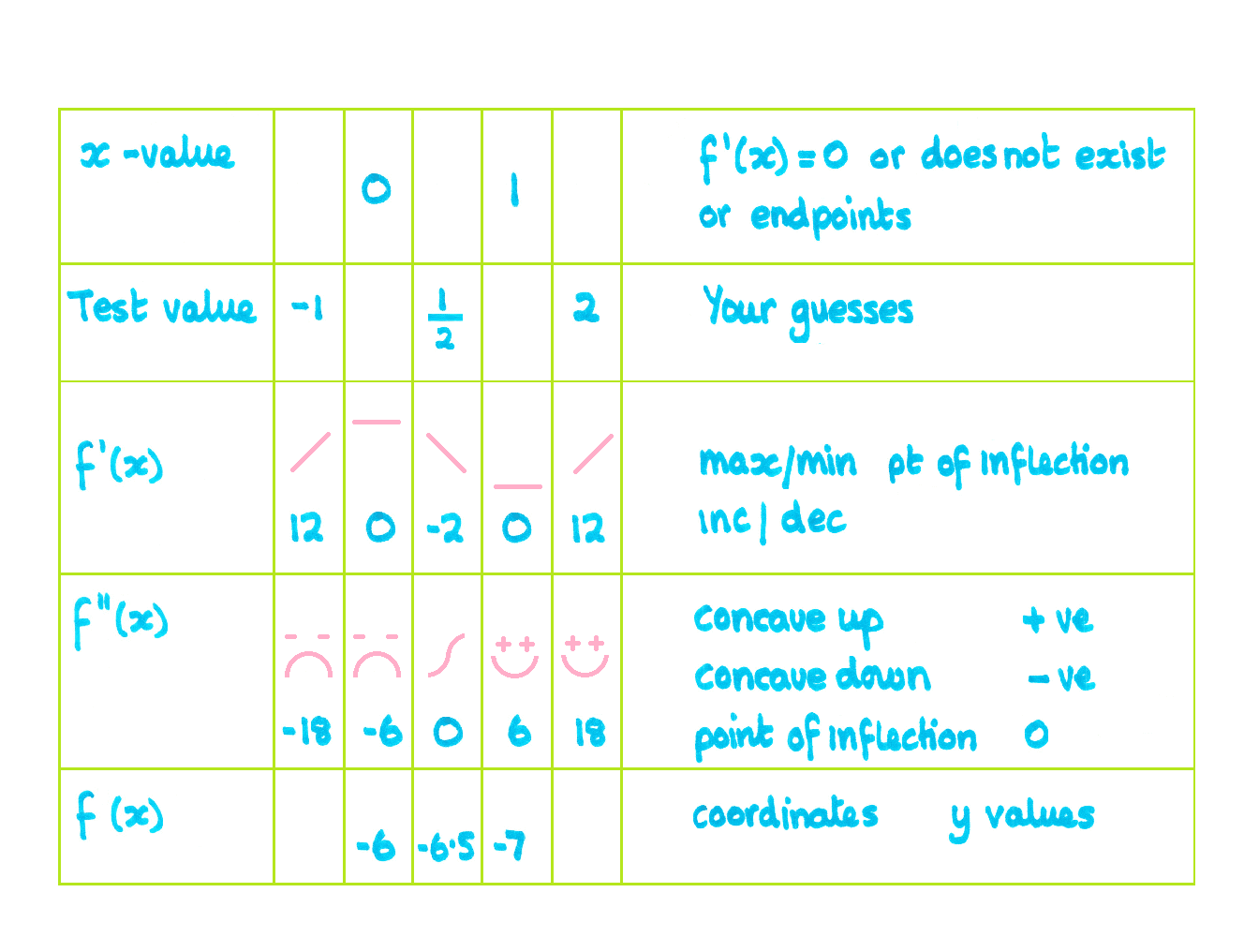
Finding Maximum and Minimum values
|
|
|
||||||||||||||||||||||||
|
|
||||||||||||||||||||||
 |
||
 |
||
 |
 |
| [Home] [Parents] [Contact us] [Services] [Mathematics] [Statistics] [School] |